
The phase space density of mass, or Distribution Function (DF) of the N-body
system was defined in Lecture 5 by considering the quantity

where
 designates the mass in the infinitesimal phase-space volume
designates the mass in the infinitesimal phase-space volume
 around
around
 at time
at time
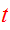 .
The DF
.
The DF
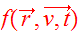 satisfies the collisionless Boltzmann Equation
(CBE),
satisfies the collisionless Boltzmann Equation
(CBE),
The collisionless Boltzmann equation describes the evolution of the
distribution function
 and it serves as the fundamental equation of collisionless N-body dynamics. In
components it is given
by
and it serves as the fundamental equation of collisionless N-body dynamics. In
components it is given
by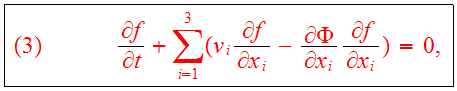
where the gravitational field
 is determined self-consistently by Poisson's
equation,
is determined self-consistently by Poisson's
equation,
Eqs. (3,4) may be viewed as a pair of coupled PDEs which together completely describe the evolution of a galaxy.
If the function
is an integral which is conserved along any orbit:
we can use the canonical equations to show that
is a steady state solution of the CBE:
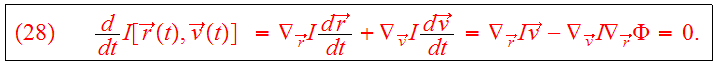
Theorem: Any steady-state solution of the CBE depends on the phase-space coordinates only through integrals of motion in the galactic potential, and any function of the integrals yields a steady-state solution of the CBE.
Proof: Suppose
 is a steady-state solution of CBE. Then
is a steady-state solution of CBE. Then
 is an integral, so that first part of theorem is true. Conversely, if
is an integral, so that first part of theorem is true. Conversely, if
 to
to
 are
are
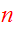 integrals, then
integrals, then

so that
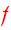 is an integral and a steady state solution of CBE.
is an integral and a steady state solution of CBE.